Aivojumppaa! Yksi tehtävä kerrallaan

[Korppi]

Eihän käy.

Eipäs käykään. Huomasin sitten ihan itsekin. :)

 

[Aleksi]

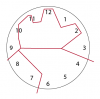
yhdessä palassa on 10, 11 ja 12 (10+1+1+1+2)
toisessa 9,1,2,3
kolmannessa 4,5,6
ja viimeisessä 7,8

Tämä ratkaisu vähän ontuu. Miksi 10 lasketaan kymppinä, mutta esim. 11 kahtena ykkösenä? Tässä vastauksessa ensimmäisen palan numeroiden summa on joko 33 tai 6. Ei siis hyväksytä.

 

[jarca]

Tämä ratkaisu vähän ontuu. Miksi 10 lasketaan kymppinä, mutta esim. 11 kahtena ykkösenä? Tässä vastauksessa ensimmäisen palan numeroiden summa on joko 33 tai 6. Ei siis hyväksytä.

Mut jos noin ei hyväksytä laskemista, niin kellotaulun numeroiden summaksi tulee 78. Neljä kertaa 15 on kuitenkin vain 60.

Edit: Vai pitääkö se yhden palan sisällä olla sitten vakiotulkinta? Eli joko kaikki yksittäin numeroina tai kokonaisina lukuina.

 

[Aleksi]

Mut jos noin ei hyväksytä laskemista, niin kellotaulun numeroiden summaksi tulee 78. Neljä kertaa 15 on kuitenkin vain 60.

Edit: Vai pitääkö se yhden palan sisällä olla sitten vakiotulkinta? Eli joko kaikki yksittäin numeroina tai kokonaisina lukuina.

Voihan se kellotaulu hajota siten, että esim. 10 menee puoliksi eli 1 toiseen palaan ja 0 toiseen. Jos 10 pysyy ehjänä, se lasketaan myös kymppinä.

 

[Cmprs]

Voihan se kellotaulu hajota siten, että esim. 10 menee puoliksi eli 1 toiseen palaan ja 0 toiseen. Jos 10 pysyy ehjänä, se lasketaan myös kymppinä.

Sitten esim. näin:
1 pala: 3+2+10
2 pala: 8+7
3 pala 9+6
4 pala 1+2+3+4+5

11 ja 12 siis hajotetaan 1+2 ja 1+1 ja siksi kolmonen ja kakkonen kahdesti. Vai ymmärsinköhän ollenkaan oikein tätä?

 

[SpaidAce]

Tästä lukujonojen ystäville:

2, 3, 6, 8, 10...

 

[.creep.]

Sitten esim. näin:
1 pala: 3+2+10
2 pala: 8+7
3 pala 9+6
4 pala 1+2+3+4+5

11 ja 12 siis hajotetaan 1+2 ja 1+1 ja siksi kolmonen ja kakkonen kahdesti. Vai ymmärsinköhän ollenkaan oikein tätä?

Jos 11 ja 12 hajotetaan 1+1 ja 1+2 eivät ole enää samassa palassa. 11 ja 12 on hajoitettava, mutta ei tuolla tavalla.

Edit: Jos heitetään fysiikanlait romukoppaan niin tuo onnistuu seuraavasti:
1. pala: (1)2+5+8=15
2. pala: 1+2+3+9=15
3. pala: 1(1)+10+4=15
4. pala: (1)1+1(2)+6+7=15

Kellotauluhan ei tuolla tavalla voi hajota, mut vastaus on ainakin oikein =)

 

[Isaskar]

Tästä lukujonojen ystäville:

2, 3, 6, 8, 10...

12,13?

 

[Beagle Boy]

Tästä lukujonojen ystäville:

2, 3, 6, 8, 10...

12, 13, 16, 18...

Kaikki alkavat k-kirjaimella.

edit. Hidas.

 

[Isaskar]

1. pala: 10+1(1)+1(2)+1+2
2. pala: (1)1+(1)2+3+4+5
3. pala: 9+6
4. pala: 8+7

Ei nyt ihan normaalit palat tuostakaan tulisi..

 

[Aleksi]

Jos 11 ja 12 hajotetaan 1+1 ja 1+2 eivät ole enää samassa palassa. 11 ja 12 on hajoitettava, mutta ei tuolla tavalla.

Edit: Jos heitetään fysiikanlait romukoppaan niin tuo onnistuu seuraavasti:
1. pala: (1)2+5+8=15
2. pala: 1+2+3+9=15
3. pala: 1(1)+10+4=15
4. pala: (1)1+1(2)+6+7=15

Kellotauluhan ei tuolla tavalla voi hajota, mut vastaus on ainakin oikein =)

Tähän tehtävään on olemassa ratkaisu, joka on mahdollinen myös fysiikan lait huomioiden. Eli palat ovat yhtenäisiä ja "liimaamalla" ne yhteen saa ehjän kellotaulun.

 

[Aleksi]

1. pala: 10+1(1)+1(2)+1+2
2. pala: (1)1+(1)2+3+4+5
3. pala: 9+6
4. pala: 8+7

Ei nyt ihan normaalit palat tuostakaan tulisi..

Kyllä tämä jo hyväksytään. Toinen vaihtoehto olisi:
1. pala: 1(0)+1(1)+12+1
2. pala: (1)0+(1)1+2+3+4+5
3. pala: 9+6
4. pala: 8+7

 

[.creep.]

Tähän tehtävään on olemassa ratkaisu, joka on mahdollinen myös fysiikan lait huomioiden. Eli palat ovat yhtenäisiä ja "liimaamalla" ne yhteen saa ehjän kellotaulun.
Tänään 21:01

Kyllä tämä jo hyväksytään. Toinen vaihtoehto olisi:
1. pala: 1(0)+1(1)+12+1
2. pala: (1)0+(1)1+2+3+4+5
3. pala: 9+6
4. pala: 8+7

Onko tuo oikea vastaus? Miten nuo palat 1. ja 2. muodostuvat, kun minun mielestä pala 1. sulkee (1)1 pala 2. ulkopuolelle?

 

[SpaidAce]

12,13?

Jep. Oli ehkä turhan helppo:)

 

[Aleksi]

Onko tuo oikea vastaus? Miten nuo palat 1. ja 2. muodostuvat, kun minun mielestä pala 1. sulkee (1)1 pala 2. ulkopuolelle?

En tiedä mikä on "virallinen" oikea vastaus, mutta noin se mielestäni ainakin ratkeaa. Eli ensimmäisessä palassa on 10:n ja 11:n eka ykkönen sekä 12 ja 1. Toisessa palassa 11:n toinen ykkönen sekä 2, 3, 4 ja 5. Kympin nolla saa myös 9:n ja 6:n palassakin. Tietysti ratkaisun "haurain" pala on juuri tuo pala 1, joka on siinä ja siinä.

Parempikin ratkaisu saattaa vielä olla olemassa. Joka tapauksessa kolmesta 2-numeroisesta kahden täytyy mennä puoliksi, että homma onnistuu.

 

[#51]

Majataloon tuli kolme miestä ja he halusivat yöpyä. Isäntä peri maksuksi kympin mieheen eli kolmekymppiä. Hän tuli kuitenkin katumapäälle ja lähetti palvelustytön viemään vitosen takaisin. Palvelustyttö otti rahan ja lähti viemään sitä miehille, mutta ajatteli, että kyllä miehille vähempikin riittäisi. Niinpä hän palautti vain kolme euroa ja piti itse kaksi euroa. Miehet olivat tyytyväisiä, kun saivat yösijan yhdeksällä eurolla.
Nyt kun lasketaan 3 kertaa 9 = 27 euroa, ja lisätään siihen tytön pihistämä kaksi euroa, saadaan 29 euroa. Mihin hävisi yksi euro?

 

[Gags]

Mihin hävisi yksi euro?

Ei mihinkään. Miehet maksoivat 27 euroa josta 25 meni huoneen hintaan ja 2 euroa meni siivoojan taskuun.

 

[tty_01]

Majataloon tuli kolme miestä ja he halusivat yöpyä. Isäntä peri maksuksi kympin mieheen eli kolmekymppiä. Hän tuli kuitenkin katumapäälle ja lähetti palvelustytön viemään vitosen takaisin. Palvelustyttö otti rahan ja lähti viemään sitä miehille, mutta ajatteli, että kyllä miehille vähempikin riittäisi. Niinpä hän palautti vain kolme euroa ja piti itse kaksi euroa. Miehet olivat tyytyväisiä, kun saivat yösijan yhdeksällä eurolla.
Nyt kun lasketaan 3 kertaa 9 = 27 euroa, ja lisätään siihen tytön pihistämä kaksi euroa, saadaan 29 euroa. Mihin hävisi yksi euro?

Alkuperäinen hinta: 30.
Alkuperäinen palautus 5 -> maksettava tulee siis 25
Palvelustyttö vetää välistä ja antaakin takaisin vain 3 -> hinta onkin 28, ja 2 euroa palvelustytön taskuun

Joskus lukioaikoina kaveri esitti samantyyppisen kysymyksen matematiikan&fysiikan opettajalle ja hän sitten vastasi, että kysymys on väärin asetettu. Mukavaa aivojumppaahan tämä kuitenkin on.

 

[Trekolmestar]

Kyllä tämä jo hyväksytään. Toinen vaihtoehto olisi:
1. pala: 1(0)+1(1)+12+1
2. pala: (1)0+(1)1+2+3+4+5
3. pala: 9+6
4. pala: 8+7

Laitetaan vielä kolmaskin vaihtoehto:

 

[tutzba]

Oli kaksi äitiä ja kaksi tytärtä. He lähtivät lomalle, ja hotellihuoneessa oli kolme sänkyä. Jokainen olisi kuitenkin halunnut oman sängyn, mutta hotellissa ei ollut yhtään lisävuoteita, eikä muissa hotelleissa ollut tilaa. Ratkaisu?

 

[Lapster]

Ratkaisu tietysti on siinä että mukana on isoäiti, äiti ja tytär. :)

 

[tutzba]

Ratkaisu tietysti on siinä että mukana on isoäiti, äiti ja tytär. :)

Näinhän se on.

 

[Riihimäki]

Oli kaksi äitiä ja kaksi tytärtä. He lähtivät lomalle, ja hotellihuoneessa oli kolme sänkyä. Jokainen olisi kuitenkin halunnut oman sängyn, mutta hotellissa ei ollut yhtään lisävuoteita, eikä muissa hotelleissa ollut tilaa. Ratkaisu?

No propleem.

Mummo nukkuu yhdessä sängyssä, tytär toisessa, ja tyttärentytär kolmannessa.
Koplassa on kuitenkin matkassa 2 äitiä ja 2 tytärtä. Eiksje?

edit. ja hidas tietty, mutta oikein meni.

 

[Lapster]

Pena, Jere, Francis ja Masa-hiiri lähtivät Saksaan hakemaan autolastillisen olutta. Takaisin Suomeen päästyään laatikot laskettiin, ja niitä todettiin olevan 236. Miehet jakoivat olutlaatikot niin, että Pena sai 20 laatikkoa enemmän kuin Jere, 53 laatikkoa enemmän kuin Francis ja 71 laatikkoa enemmän kuin Masa-hiiri. Kuinka monta laatikkoa kukin sai?

 

[teemu73]

Kuinka monta laatikkoa kukin sai?

Pena 95
Jere 75
Francis 42
Masa 24